Brouwerの不動点定理と(位相幾何版の)角谷の不動点定理が直観的には「明らか」な理由
#数楽 もしかしたら、位相幾何版の角谷の不動点定理(Brouwerの不動点定理の一般化)を使ったせいで、何か直観的に意味不明なことをやっているように感じた人が多いかもしれない。しかし、角谷やBrouwerの不動点定理は直観的には当然成立するべき定理なので実際にはそうではない。
#数楽 ブラウワーの不動点定理と位相幾何版の角谷の不動点定理はそれらが成立しないと同じ方法で「ありえない連続写像」を作れてしまうことによって証明可能。どのような連続写像が「ありえない」かについては直観的に納得可能。続くhttps://twitter.com/genkuroki/status/841120263743848448 …


#数楽 続きBrouwerの不動点定理の証明は添付画像の通り。Brouwerの不動点定理が成立していないならば「ありえない連続写像φ」を作れてしまう。作れるはずがないのでBrouwerの不動点定理は成立する。pic.twitter.com/LDVUa5uy8k

#数楽 続き。位相幾何版の角谷の不動点定理が「当然なり立つべき結果」もBrouwerの不動点定理のケースとほぼ同じ。ただし、閉円盤Dそのものだけではなく、D を縦方向に伸ばして「厚み」を付けた Γ も考える。pic.twitter.com/RplLaDQpYs

#数楽 続き。位相幾何版の角谷の不動点定理の証明の方針の直観は本質的にBrouwerの不動点定理の場合と全く同じ。扱っている図形の厚みが至る所ゼロであろうが、引き伸ばされて「厚み」がゼロで無くっている点があっても「切り裂く必要があるか否か」は変わらない。pic.twitter.com/EFCWaAH3BI
#数楽 位相幾何では図形の「繋がり具合」を問題にするのですが、厚みがない図形に厚みをつけたり([0,1]と直積を取る)、厚みを無くしたり、毛を生やしたり、毛を剃ったり、……の操作で変化しない「繋がり具合」を扱うことが極めて普通によくある。ホモトピー同値の目で図形を眺めること。
#数楽 角谷の不動点定理について検索すると経済学への応用がたくさんヒットするのですが、不動点定理の類の道具が何か高級な道具のような扱いになっていて、「直観的には当然そうなるべきなので、当然成立そうなると考えて先に進む」というスタイルの解説を見付けることができませんでした。続く
#数楽 続き。数学を応用するときには、数学的結果を「ブラックボックス的」に扱って「よくわからない結果を正確に応用する」という態度では不健全になりやすいと思う。「直観的に当然そうなるべき結果」という扱いで応用する場合の方が健全でわかりやすい議論になりやすいと思う。
#数楽 Brouwerの不動点定理およびその角谷的一般化の類は、数学的に厳密な証明を知らなくても、直観的に当然成り立つべき結果だと感じられるような話なので、応用するときにはそういう態度で精神的に気軽に応用して欲しいと思いました。
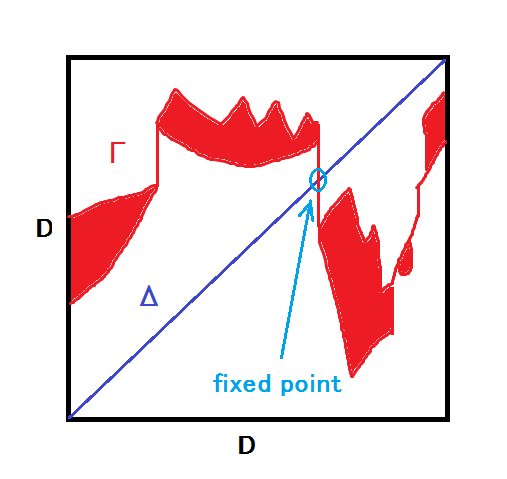
#数楽 Kakutaniの不動点定理についてはこのツイートに添付した画像も参考になると思います。正方形の一辺がD(の模式図)で赤で書いたギザギザした部分がΓ(の模式図)です。連続写像p:Γ→Dは縦向きの射影。この図で斜め45度線とΓが交わることは自明。pic.twitter.com/0GgEihmJeK

#数楽 Γは正方形の下辺Dを縦方向に引き伸ばした形になっています。ただし引き伸ばし方は場所によって異なります(Γ→Dのファイバーが可縮)。角谷の不動点定理ではこのような状況で「対角線とΓが共通点を持つ」という主張です。pic.twitter.com/0GgEihmJeK
#数楽 数学者が書いた教科書に数学的に厳密な証明が書いてあることは不思議でも何でもないし、数学者はそういう文献を生産する社会的役割を担っていると思うのですが、数学を応用することを専門としている人達が直観的に明らかな理由の説明よりも厳密な証明の説明の方を優先するのはおかしいと思う。
#数楽 しかし、へたをするとテキトーなことを言っていると思われてしまうような直観的な説明の仕方を躊躇無くできるためには、論理的スキルに自信がないと難しいと思う。やはり人間、間違うのは怖いです。しかし、そういう理由で厳密な証明の説明しかしないのはとても不健全だと思う。



